선형 모델과 회귀분석의 직관적 이해 (1)

18세기 말 인류 최고의 수학자 가우스가 정규분포와 최소제곱법을 만든 이후로, 선형 모델(Linear Model)은 다양한 방향으로 진화했고 발전해왔다.
20세기 이후 컴퓨터 계산과 모델링 기법의 발전에 힘입어, 소위 말하는 “빅데이터” 시대에 복잡한 계산까지 해줄 수 있는 “머신러닝”, ”딥러닝”이 각광을 받고 있다.
데이터 분석가나 데이터 사이언티스트가 되고 싶은, 혹은 이미 현업에 있는 분들의 상당수가 머신러닝, 딥러닝에 열광하고 이를 적극적으로 활용하지만, 선형 모델과 회귀분석에 대해서는 그저 “단순한 것”, “올드 스쿨(Old School)”로 여기는 경향이 많다.
그러나, 220년이 넘도록 선형 모델의 중요성은 이 순간에도 변하지 않았다. 딥러닝을 포함한 모든 최신 기법들은 하늘에서 갑자기 뚝 떨어진 것이 아니다. 이들은 선형 모델에 적당한 커널(Kernel)을 사용해 비선형으로 매핑하거나, Tree Model과 같이 직선으로 파티션을 나눠 비선형 패턴을 만드는, 결국 선형 모델에 트릭을 써서 일반화한 것에 지나지 않기 때문이다. 따라서 비선형 모델링을 잘 하기 위해서는 선형 모델 및, 대표 분석법인 ‘회귀분석’에 대한 이해가 필수적이다.
향후 기회가 될 때마다 데이터 사이언티스트들이 필수적으로 알아야 할 “선형 모델”과 “머신러닝” 기법들에 대해, 개념이나 코드 예제보다는 핵심을 찌를 수 있는 “직관” 위주로 글을 투고하려 한다.
첫 번째 글에서는 “선형 모델”이 무엇인지 살펴보고, 선형 모델을 다루는 대표적인 분석법인 “선형 회귀분석(Linear Regression Analysis)”의 필요성에 대해 소개하겠다.
Myth: 선형 모델에 대해 가지는 환상
다음 예시에서 비선형 모델은 몇 개일까?
(1) $y_{i} = \beta_{0} + \beta_{1}x_{1i} + \beta_{2}x_{2i} + \epsilon_{i}$
(2) $y_{i} = \beta_{0} + \beta_{1}x_{1i} + \beta_{2}x_{1i}^{2} + \beta_{3}x_{1i}^{3} + \epsilon_{i}$
(3) $y_{i} = \theta_{1}e^{\theta_{2}x_{i}} + \epsilon_{i}$
(4) $y_{i} = \frac{\theta_{1}x_{i}}{\theta_{2} + x} + \epsilon_{i}$
(5) $\frac{d y_{i}}{dt} = \alpha y_{i}$
(6) $y_{i} = \alpha_{0} + \sum_{i=0}^{n}\alpha_{i}K(x, x_{i}) + \epsilon_{i}, K(x, x_{i}) = e^{-\gamma ({x - x_{i}})_{2}^{2}}$
눈치가 빠른 사람들은 짐작했겠지만, 가장 마지막 (6)을 제외한 (1) ~ (5)는 모두 선형 or 선형으로 변환 가능한 모델이다. 다수는 (1)이 선형이라는 것에는 공감을 하지만, (2) ~ (5)가 선형이라는 것에는 고개를 갸우뚱할 수도 있을 것 같다.
여기에서 선형 모델의 정의에 대해 짚고 넘어가자.
[모델의 선형성]
모델이 “선형(Linear)”이라는 것은, 추정해야 할 파라미터(Parameter)에 대해 “선형변환”을 만족시키는 것으로 정의한다. 이 때, 내가 가지고 있는 변수(Variable)들은 꼭 일차식일 필요가 없다.
[선형변환]
실변수 벡터공간(Vector Space)에서, 벡터 X, Y와 스칼라 a에 대해 다음을 만족하는 함수 T를 선형변환(Linear Transformation)으로 정의한다.$T(aX + Y) = aT(X) + T(Y)$
여기에서 벡터 X, Y를 각각의 식으로 분리해 계산할 수 있는 성질을 “가산성(Additivity)”이라 하고, 스칼라 a를 식 밖으로 분리할 수 있는 성질을 “동질성(Homogeneity)”이라 한다.
(1)이 선형성을 만족시키는 것은 자명하다. 이는 “다중 선형회귀모델(Multiple Linear Regression Model)”을 나타낸 식이며 다음 글에서 언급할 기회가 있을 것이다.
흔히들, (2)의 경우는 제곱 및 세제곱 항까지 사용했는데 왜 “비선형”이 아니냐고 오해한다. 다시 정리하자면, 모델이 “선형”인지 “비선형”인지는 우리가 추정해야 할 “파라미터”가 일차식인지 확인하면 된다. $\beta$ 값들은 전부 일차식이고, 따라서 이는 변수 벡터 $[1, x, x^2, x^3]$의 선형결합(Linear Combination) 형태로 나타낼 수 있으므로 선형이다. 마찬가지로, 모든 다항식 모델은 “$a * x^{n} + b * x^{n-1} + … + q * x + r * 1$” 꼴로 나타낼 수 있으므로 “선형”이다.
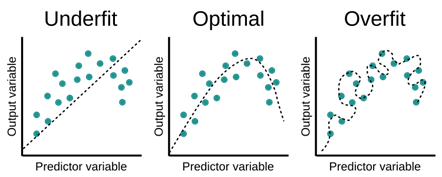
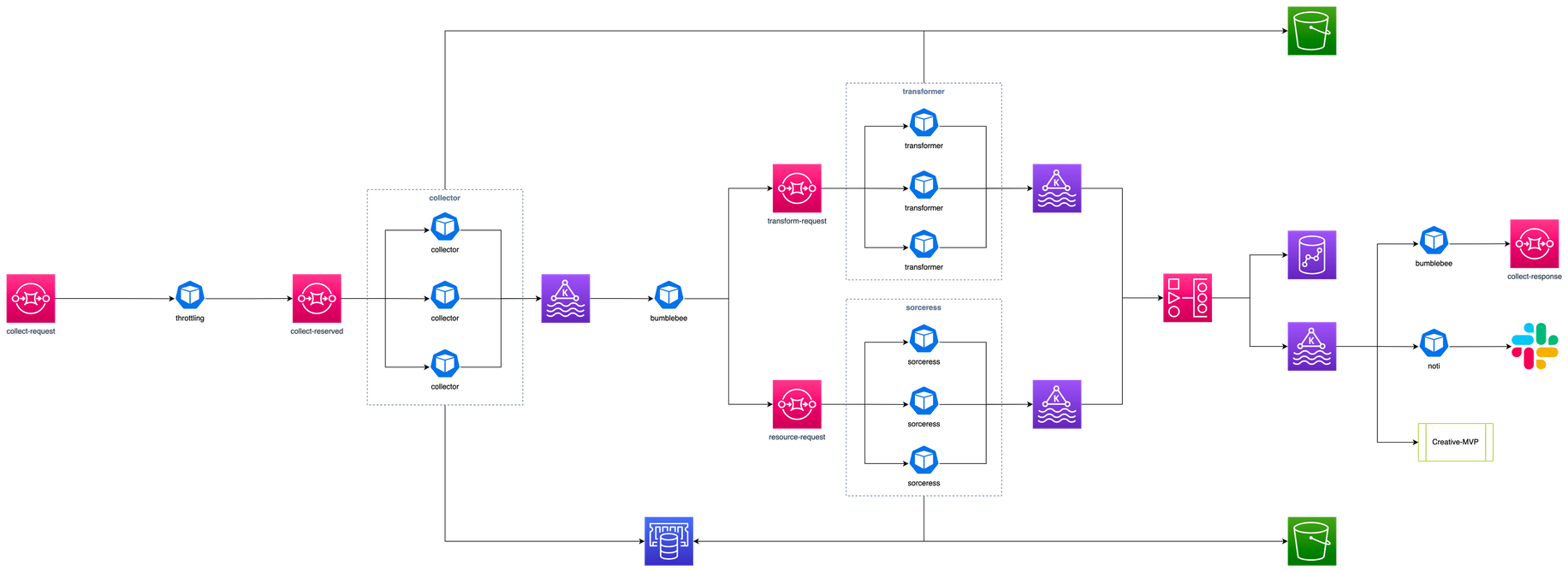
위 그림의 Overfit 케이스도 선형 모델로 나타낼 수 있을까? 정답은 “그렇다”이다.
우리가 중, 고등 수학에서 미지수가 n개인 방정식을 맞추기 위해서는 n개의 식이 필요함을 이미 배웠다. 이에 따라 두 점만 있으면 직선으로 연결할 수 있고, 세 점은 이차함수, 네 점은 삼차함수, … 결정적으로 n-1차 다항식으로 모델링을 하면 n개의 점을 100% 완벽하게 맞출 수 있다.
(물론 이렇게 모델링을 하면 bias는 0으로 만들 수 있어도, variance가 매우 커지게 되어 MSE(Mean Squared Error) 관점에서는 좋지 못한 모델일 것이다.)
(3)의 경우 겉보기에는 맞춰야 할 파라미터 $\theta$가 지수 꼴로 나타나 있어 비선형으로 보인다. 그러나 양변에 로그를 취하면 $\log(y_{i}) = \log(\theta_{1}) + \theta_{2}x_{i} + \log(\epsilon_{i}) = \beta_{0} + \beta_{1}x_{i} + \epsilon_{i}^{*}$과 같은 식이 되어 변수 벡터 $[1, x]$을 이용해 $\log(y)$를 추정하는 식으로 변형할 수 있다.
(4)의 경우도 마찬가지다. 분모와 분자에 역수를 취하는 트릭을 사용하면, $\frac{1}{f(x, \theta)} = \frac{x_{i} + \theta_{2}}{\theta_{1}x_{i}} = \frac{1}{\theta_{1}} + \frac{\theta_{2}}{\theta_{1}}\frac{1}{x_{i}} = \beta_{0} + \beta_{1}x_{i}$ 식과 같이 선형 꼴로 정리가 가능하다.
(5)는 미분 연산자가 들어가 있는데 왜 선형일까? 놀랍게도 미분과 적분 연산자 또한 선형변환의 성질을 만족시킨다. (고등학교 때 상수항을 미적분 기호 밖으로 자유자재로 빼거나, 두 식들을 따로 분리해서 쉽게 계산을 한 경험이 있을 것이다.)
위 식은 미분방정식에서 가장 쉬운 예시로, 식을 정리하면 (3)과 유사한 지수함수 형태로 정리되어 (3)과 마찬가지로 선형으로 변환이 가능하다.
엄밀하게는 (3) ~ (5) 식은 그 자체로 선형이 아니지만, 간단한 트릭을 사용하면 선형 모델처럼 취급이 가능하다는 뜻에서 “본질적으로 선형인(Intrinsically Linear)” 모델이라고 한다.
항상 참은 아니지만, 선형화가 가능할 경우 선형으로 모델을 변환하면, 아래에서 언급할 선형 모델의 많은 장점을 활용할 수 있어 유리하다.
(6)은 머신러닝 모델인 서포트 벡터 머신(Support Vector Machine)에서 Gaussian Kernel을 사용한 형태로 대표적 비선형 모델 중 하나다. 추후 머신러닝 모델들에 대해 얘기할 때 중요하게 다룰 것이다.
선형 모델의 장점
선형변환의 대표 성질인 가산성과 동질성을 만족시키는 선형 모델은 매우 중요하다.
-
복잡한 모델을 쉬운 계산들로 분해할 수 있다: 단순한 변수들의 합과 상수배만으로, 모델들을 기초적으로 분리해 따로 계산이 가능하다. 이러한 특징을 이용해 선형의 특징을 살리면 “계산이 매우 편리하다”.
-
모델의 해석이 쉽고 직관적이다: 선형변환의 특징 중 “동질성”을 생각해보자. 단순히 변수 x가 a배가 되면, 결과도 a배만큼 커진다. 우리는 선형 모델에서 변수에 multiplier 역할을 하는 파라미터에 관심이 있다. 가령 “내가 광고비를 2배만큼 증액했을 때, 신규 설치는 얼마나 증가할까?”와 같이 내가 집어넣은 변수의 효과의 크기에 관심이 있거나, 혹은 “페이스북 메신저 지면에 광고를 하는 것은 효율에 긍정적일까, 부정적일까?”와 같이 의사결정을 위해 효과의 부호에 관심이 있을 수 있다. 선형 모델을 통해 파라미터를 도출하면 파라미터를 그대로 해석할 수 있기 때문에 모델이 매우 간단하다. ($\frac{\partial y}{\partial \beta_{i}} = c$와 같이 상수로 도출됨을 생각해보자. “뿌린 만큼 거둔다”의 원리가 선형 모델에 숨어있다.)
-
복잡한 패턴을 요구하지 않는 데이터에서 견고(Robust)한 추정이 가능하다: 항상 그렇지는 않지만 (선형 모델에서도 얼마든지 변수에 다항식, Kernel 트릭을 가해 직선이 아닌 “곡선”을 만들 수 있으므로), 일반적으로 복잡한 패턴을 다루기 위해 사용하는 비선형 모델 대비, 선형 모델을 잘 쓰면 오버피팅(Overfitting ; 미래 데이터를 잘 맞추지 못하는 것)을 방지하고 파라미터 및 예측값에 대해 “견고한 추정”을 할 수 있다.
머신러닝에서 강조하는 MSE 분해 식에서도, $bias^{2}$와 $variance$를 동시에 고려하는 것이 중요하다는 것을 보여주고 있다. 꼭 비선형 모델을 써야 하는 데이터가 아닌 이상, 비선형 모델을 무분별하게 쓰는 것은 추정의 variance를 지나치게 높여 MSE를 망치게 하는 원인이 된다. (그렇다고 선형 모델이 bias를 0으로 만들지 못하는 것도 아니다)
이와 같이 선형 모델은 최소 계산비용(Computational Cost)이 비선형 모델 대비 매우 우수하다는 장점이 있고, 더 나아가 특정 조건을 만족할 경우 비선형 모델을 포함해 “가장 좋은” 모델이 될 수도 있는 잠재력도 가지고 있다. 앞으로 선형 모델의 대표적인 분석 기법인 “선형 회귀(Linear Regression)”에서 이를 언급할 것이다.
선형 회귀분석: 조건부 기댓값의 원리
다음 데이터를 어떻게 요약할 수 있을까?
캠페인별 클릭 수: $[100, 100, 90, 80, 70, 60, 40, 30, 30, 20, 10, 30, 40, 70, 50]$
아마 다들 자연스럽게 “데이터의 개수는 15개, 클릭 수의 평균은 54.7건” 이라고 생각했을 것이다. 이처럼 우리가 평균을 바탕으로 데이터를 요약하고 예측하는 것은 매우 자연스럽다.
새로운 캠페인을 세팅해 클릭 수를 예측해야 한다고 하자. 현재 아무 정보가 없는 상태에서, 새로운 캠페인에서 기대할 수 있는 클릭은 몇 건이라고 생각하는 것이 합리적일까? 지금까지 가지고 있는 정보로는 클릭 수의 평균이 54.7건이었으므로, 새 캠페인의 클릭 수도 약 54.7건이지 않을까? 라고 예측하는 것이 가장 합리적일 것이다.
다들 눈치챘겠지만, 이는 좋은 예측이 아니다. 아무 정보도 없는 상태에서도 누구나 예측할 수 있는, “그나마 최선” 인 숫자인 것이다.
이 “단순 찍기” 모델이 얼마나 못 맞췄는지 측정하기 위해, 맞추지 못한 만큼인 “잔차(Residual)”의 분산을 구해보자. 표본분산 공식 = $\frac{1}{(n-1)}(\epsilon_{i} - E(\epsilon_{i}))^{2}$에 값을 대입하면 약 855.24라는 값이 나온다.
우리는 고등학교에서 변수 x에 적당한 숫자 a를 더하더라도, x의 분산과 (x + a)의 분산은 같다는 것을 배웠다. 우리가 값을 “상수” 값으로만 추정했기 때문에, “단순 찍기” 모델의 분산은 데이터 자체의 분산과 같은 것이다.
잔차의 분산은 우리가 예측하지 못한 “불확실성”이나 다름없다. 모든 통계적 데이터 분석의 목표는 불확실성으로 대표되는, 바로 이 분산을 줄이는 것이다. 에러의 분산을 줄여 좀 더 데이터를 잘 맞추려면 어떻게 해야할까? 데이터를 설명할 수 있는 “정보”가 필요하다.
만약 더미변수(Dummy Variable)로 “레버를 활용한 캠페인”은 T, 그렇지 않으면 F인 정보가 추가로 주어졌다고 하자. 이 변수에 대한 벡터 $X = [T, T, T, F, F, T, F, F, T, F, F, F, F, T, F]$ 라면 이 정보를 활용해 데이터를 조금 더 잘 설명할 수 있다.
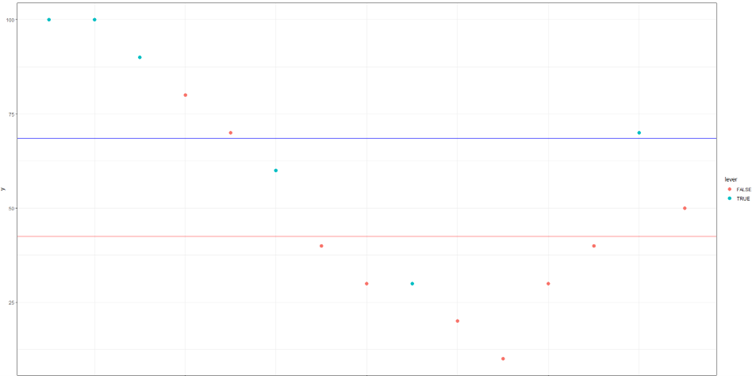
“레버 마케팅 유무” 라는 정보에 따라, 각각의 조건부 기댓값(Conditional Expectation)을 계산하였다. 이를 통해 예측한 클릭 수는, 레버 마케팅을 적용한 캠페인은 “평균 68.6건(파란 선)”, 그렇지 않으면 “평균 42.5건(붉은 선)”으로 나타난다. 이는 무정보일 때였을 때 대충 예측한 “54.7건”보다 정확하다.
데이터 분석가, 또는 퍼포먼스 마케터라면, 누구나 엑셀에서 “피벗 테이블”이라는 멋진 기능을 사용해본 경험이 있을 것이다. 그렇다면 피벗 테이블은 왜 쓰는가? 우리는 피벗 테이블에서 성과를 분석할 때 왜 “세그먼트” 단위로 조건들을 나누어 성과를 분리해 측정하는가?
우리는 감각적으로 “세그먼트를 나누어” 성과를 분석하는 것이 더 정확함을 알고 있기 때문이다.
여기서 조건부 분산에 대한 주요 성질을 짚고 가자. 조건부 분산은 아래와 같이 분해가 가능하다.
[조건부 분산의 분해]
변수 $Y, Z$에 대해, $V(Y) = E(V(Y|Z)) + V(E(Y|Z))$가 성립한다.
그런데 분산은 항상 0 이상의 값이므로, 어떤 변수 $Z$가 주어져 $E(Y|Z)$를 계산할 수 있다면, $V(Y|Z)$는 0 이상이므로 $E(V(Y|Z))$ 역시 양수이고, 따라서 $V(E(Y|Z))$는 $V(Y)$보다 작거나 같은 값을 가진다.
결국 $E(E(Y|Z))$는 이중 기댓값 정리(Law of Iterated Expectation)에 의해 $E(Y)$와 같으므로, $E(Y|Z)$는 $E(Y)$와 평균은 같으면서, 분산은 더 작은 좋은 추정량이 된다.
이에 대해 조금 더 상세하게 알고 싶다면 Rao-Blackwell Theorem을 참조하면 된다. 내용은 어렵지만, 정리의 핵심은 파라미터를 잘 추정할 수 있는 “정보”가 주어진다면, “정보”를 조건으로 활용해 조건부 기댓값을 구하는 것이 분산(불확실성)을 줄여주므로 더 합리적이라는 것이다.
실제로 “레버 마케팅 유무”였던 $X$를 정보로 걸었을 때, 잔차의 분산은 673.98로, 무정보 상태에서 단순 평균으로 예측했을 때 잔차의 분산인 855.24 대비 78.8% 수준으로 약 21.2% 개선된 것을 확인할 수 있다. 추후 잔차 분산의 개선율 0.212에 대해 다시 언급할 기회가 있을 것이다.
이처럼 데이터를 설명하거나 예측할 때, 정보 $X$를 바탕으로 한 합리적인 조건부 기댓값(평균)을 구하는 기법을 “회귀분석(Regression Analysis)”이라 한다.
마치며
지금까지 선형 모델의 정의와 회귀분석의 당위성에 대해 알아보았다. 모든 모델과 분석법은 갑자기 태어난 것이 아니라, 쉬운 것에서부터 점차 필요에 의해 발전하며 탄생하였다.
다음 글에서는 다소 어려울 수 있지만, 회귀분석 추정법 및 성질에 대해 다루도록 하겠다.